Excentricité d’un sommet

Les réseaux sociaux représentent des relations comme les contacts ou l’amitié entre individus, les communications dans un groupe, les transactions entre compagnies. Trouver les acteurs importants, découvrir les groupes ou les communautés soudés, identifier les similitudes sont autant d’exemples d’analyses qui peuvent être menées sur les réseaux sociaux.

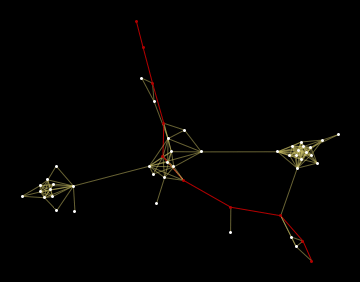
L’excentricité d’un sommet donne le plus long des plus courts chemins qui vont de ce sommet à tous les autres sommets du graphe.

VertexEccentricity_1.gif 52 51 50 49 48 47 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1

L’excentricité du sommet 10 (tout en haut) vaut 9. Le plus long des plus courts chemins qui permettent d’atteindre tous les autres sommets comporte 9 étapes. Le chemin représenté part ici du sommet 10 et aboutit au sommet 52.
N. B. Le survol d’un sommet donne son nunéro dans une infobulle.

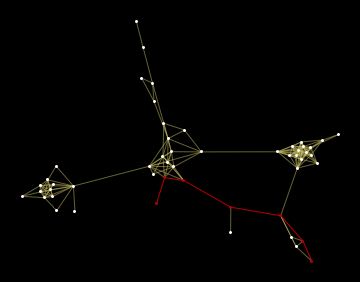
VertexEccentricity_2.gif 52 51 50 49 48 47 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1

L’excentricité du sommet 20 vaut 6. Le chemin représenté est le plus court pour relier le sommet 20 au sommet 52. Il comporte 6 étapes.

Le langage Mathematica permet de modéliser et d’analyser des réseaux. Des fonctions de haut niveau détectent les communautés, trouvent les groupes à forte cohésion et visualisent les résultats.

Created with the Wolfram Language

Valid XHTML 1.0 Strict